kalman

kalman 滤波器

一直没深入看一下kalman，今天查阅了很多资料，终于找到一个很形象很具体的解说

如何通俗并尽可能详细地解释卡尔曼滤波？ - 云羽落的回答 - 知乎

matlab原版

其实解释起来不复杂

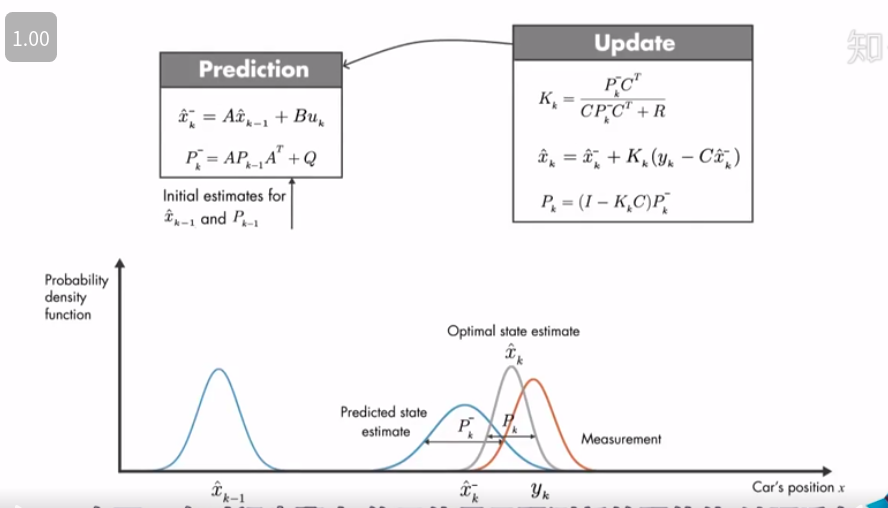
1. 预测变量x, 但是有两个x,怎讲？因为x的真实值我们是永远不知道的，就算温度计测出来的温度也有误差哦。\( y_k \) 测量值，温度计测出来的，\( \hat{x}^{-}_k \) 这是通过数学模型估算出来的值，\( \hat{x}_k \) 就是kalman最优估算值，需要得到的值

2. 有两个协方差，和上面对应，一个测量R，一个模型估算\( P^{-}_k \)，kalman最优估算值是\( P_k \)。Q对应transition_covariance(pykalman)，Q是mean为0，方差为Q的高斯分布，pykalman中的这个参数命名有点问题，这个不是协方差，其实就是P在变化时的一个噪声，应该是variance。而P是描述状态变量间(多维)关系的，初始P为initial_state_covariance(pykalman)。R和P不一样，R和Q功能一样，为observation_covariance(pykalman)。

3. 有一个增益K，就是通过两个协方差计算而来，其实简单来讲就是把测量值 和 模型估算值 做一个中和

4. 注意：

   • 当然，可以用多个传感器来提高精确度
   • 普通kalman滤波器只支持线性，而且状态值x要符合高斯分布，貌似只要噪声项为高斯即可，这个再考察一下。

一些参数，图片来源

1. \( A_t \) 就是 transition_matrices ，状态转移矩阵
2. \( B_t \) 是 contral_matrices 控制矩阵
3. \( C_t \) 是 状态转移矩阵，从state到observation的线性计算矩阵,observation_matrices
4. \( \epsilon_{t} \) 对应上上图的Q，transition_covariance，图中的解释为Rt可能是另外的公式，那么\( \delta_{t} \) 就是对应上上图的R了，observation_covariance，图中的解释为Qt是另外的公式

实例

实例 notebook 展示

moving average

这个貌似有点问题，因为价格本身不是高斯分布

linear regression