自然分布

概念

这不是正态分布吗？是的。英文Normal distribution，还叫高斯分布。Normal distribution这个直译应该是正常分布，可能当时某位学者翻译时觉得正常分布这个名字不高大上，所以用了正态分布。但是看完这篇文章，你会觉得自然分布才是最佳命名。

本来想引用一下wiki里面的一些解释，全是公式，算了，公式不是这篇文章的目的。先来看一下全球智商的概率分布图。

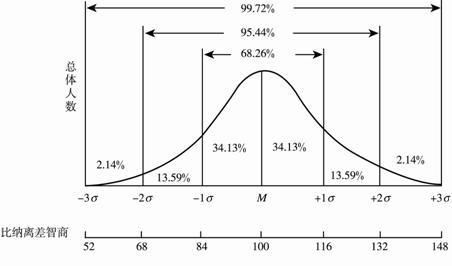
这时候大家是不是先去测一下智商，我当时看到这张图就去测了一下，结果还凑合，和我在现实生活当中的自我估计值差不多。

100 为均值，也为期望值，图中的M。也就是大家的智商都是靠向100的，从统计学来讲，我们生的孩子智商都是向100靠拢的。

这时候有人问了，那么智商为100的概率是多少呢？具体多少我也不会算，正态分布是连续概率分布，一般不用于计算单个点的概率，主要用于某个区间概率的计算。

100为均值，这样大于100的概率为50%，小于100的概率为50%，不要问我等于100的情况哪里去了，上面说了不考虑单点概率。还好我的是在右边的50%。

更细致的解读下，智商在100和116之间的概率为34.13%，智商大于132的概率只有2.14%，100个人中只有2个人智商大于132，非常稀少，我也不是。

下面还有一个横坐标是什么呢？-1σ这些是啥？

σ是标准差，公式大家可以自行搜索，中文表示为：各个属性值减去均值(100)的平方和除以属性值的个数，再开平方，不开平方的叫方差。

在金融行业里面经常用标准差来表示某个时间序列（也可以理解为某支股票）的波动率。为什么不用方差呢？因为方差里面的计算因子是经过平方的，再开个平方最接近于真实波动率。

图中显示的标准差就是16。

生活应用

智商分布如此，其他呢？身高，体重，都是这样的，还有学校单次考试成绩的分布，公司里面工资的分布，当然这些不敢说完全服从正态分布，因为样本数量，群体特性等原因，但都者近似正态分布。自然世界中很多属性的概率分布基本都近似正态分布，所以叫自然分布是不是更合适，当然自然分布也是统计学的核心。

在一个团队中，可以把人从多方属性进行统计，忠诚度，工作能力，搞事能力等等。如果不是在招聘时特别针对某项属性进行了筛选，那么是不是大部分的人其实都是中等水平，而且出现少数高于正常水平的和少数低于正常水平的也是一个正常现象。

在某一天发完工资后，偷偷的和小伙伴们一讨论，为什么我和大部分的人一样呢？愤愤不平。这时候自然分布告诉我们，我们起码有68%的概率工资都在一个普通区间内，是不是一下就平衡了。当然如果你想超越这68%那就得加倍努力，诶，努力程度如果可以量化的话是否也是自然分布呢？我没试过，但是应该是。

为什么世间会有如此有意思的统计学原理呢？这个嘛，我也不太清楚。

代码实践

下面我想做一个针对上证指数分布的代码尝试，比较基础，大师们和不想看代码的朋友可以先撤了。

这时候有朋友会问？如果上证指数也服从正态分布，那么会有一个均值，假如是4000点，那么上证指数会永远在4000点附近转悠吗？根据经济学原理，现在每年CPI好歹也有个3左右，这不科学啊。

好问题，看代码一步步的分析起来，本测试采用了上证指数2008.1.1到2018.1.1 10年的日线数据，数据可以从QuantOS上面获取。

1. 上证指数

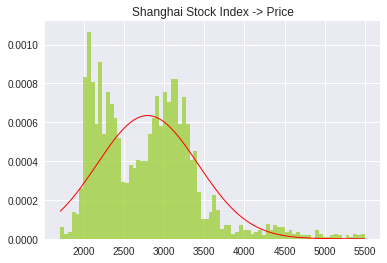
红色的是标准正态分布线，绿色的是真实分布，上面那位提出疑问的朋友说中了，并不是正态分布，连近似都不是，不知道是个什么分布，类似于方波信号（1和-1）的分布，两个尖儿，按经济学原理来讲，数据时间越长，尖儿越多。

Python代码如下：

# shts为上证指数每日收盘点数的时间序列

# 画正态分布红线
draw_guass(shts) 

plt.hist(shts,80,normed=1,histtype='bar',facecolor='yellowgreen',alpha=0.75)
plt.title(u'Shanghai Stock Index -> Price')
plt.show()

2. 价差

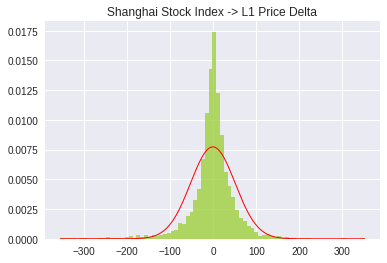
先对上证指数做了一阶差分，然后再做统计。简单来讲就是测试一下上证指数每天价格变化量的分布。

# shts_diff_l1 上证指数每日收盘点数的1阶差分时间序列
shts_diff_l1 = shts.diff().dropna()

draw_guass(shts_diff_l1)
plt.hist(shts_diff_l1,normed=1,histtype='bar',facecolor='yellowgreen',alpha=0.75)
plt.title(u'Shanghai Stock Index -> L1 Price Delta')
plt.show()

现在再来看看，是不是有点意思了，再想想我们其实对收益更感兴趣。

3. 简单收益率

ts_simple_rate = ((shts - shts.shift(1))/shts.shift(1)).dropna()

draw_guass(ts_simple_rate, width=0.001)
plt.hist(ts_simple_rate, 40, normed=1,histtype='bar')
plt.title(u'Shanghai Stock Index -> Simple Return')
plt.show()

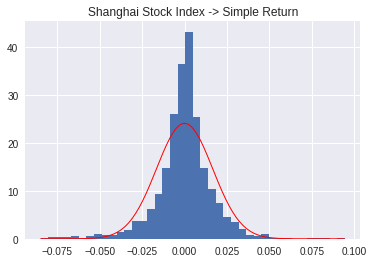
收益率其实已经很接近正态分布，当然尖锋特别明显，这也表明我国股市处于无力振荡的时间真的很长啊...

其实在金融领域大都采用对数收益率，对数收益率有可以做方便统计的加减运算等等很多优点，下面我们来做一下对数收益率的分布统计。

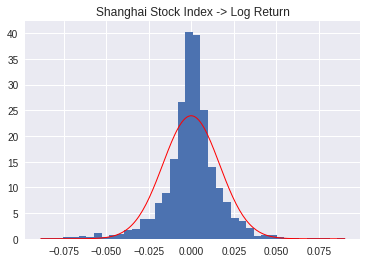
4. 对数收益率

ts_log_return_rate = np.log(shts/shts.shift(1)).dropna()

draw_guass(ts_log_return_rate, width=0.001)
plt.hist(ts_log_return_rate, 40, normed=1,histtype='bar')
plt.title(u'Shanghai Stock Index -> Log Return')
plt.show()

尖锋比简单收益率小了一些，不过大体形状上类似。

最后基于上证指数做的统计测试，只是我学习的一个案例，不过对于小菜鸟的我前前后后也花了不少的功夫，大师们可以完全绕过，也希望菜鸟朋友门可以把统计学这门基础学好，慢慢来，不要着急。

自然分布存在于世间万事万物，这也让我在最近的学习中体会到了数学之美。我又想到了查理芒格提到的，多学习一些普世科学，不要局限于一个领域内，会对我们有非常大的帮助。我觉得基础统计学应该算一门普世科学。