一. 介绍

pairs trading wiki

论文下载

这篇论文是可以从 wikipedia 上的 pairs trading 词条里面的 Model-based pairs trading 部分找到，说明这只是一篇入门级的论文。但是真TM难啊，我苦苦读了接近两个月的金融随机分析就是为了看懂这篇论文，现在还在补基础数学......

二. 把问题公式化

定义资产

无风险利率r的资产

$$dM(t)=rM(t)dt \qquad (1)$$

为什么是这个样子的呢？

因为 \(M(t)=e^rt \quad\Rightarrow\quad M'(t)=re^rt=rM(t) \quad\Rightarrow\quad M'(t)=\frac{dM(t)}{dt}=rM(t)\)

其实上面是求一个微分方程，我是根据经验猜出来的

股票A和股票B

其中股票B是遵守几何布朗运动(GBM)的资产

$$dB(t)=\mu B(t)dt+\delta B(t)dZ(t) \qquad (2)$$

其中\(\mu \)是漂移量，\(\delta \)是波动，Z(t)是一个标准的布朗运动。

这里要注意，GBM和标准的BM是不一样的，他们求微分所对应的伊藤公式也是不一样的。

股价对数的差(spread)

$$X(t)=ln(A(t))-ln(B(t)) \qquad (3)$$

假定 X(t) 遵守 Ornstein-Uhlenbeck process

$$dX(t)=k(\theta -X(t))dt+\eta dW(t) \qquad (4)$$

\(k(\theta -X(t)) \) 是瞬间价差的变化，\(\theta \)是长期需要回复到的平均值，也可以说是期望值，k表示回复平均的速度，\(\eta \)是波动，标准差。

看到这里知道为什么用Ornstein-Uhlenbeck过程了吧，因为配对交易就是价差回归的一个过程，这个OU过程就是一个均值回归的一个过程，刚好一致。

股票A

上面只给出了股票B的随机微分方程，所以根据 (2)(3)(4) 和 伊藤引理，可以求出

$$dA(t)=(\mu +k(\theta - X(t)) + \frac {1}{2}\eta^2+\rho\delta\eta)A(t)dt+\delta A(t)dZ(t)+\eta A(t)dW(t) \qquad (5)$$

作者就一句话就出来了，我的计算过程如下：

对 (3) 式两边同时对t求微分

$$ dX(t) = dln(A(t)) - dln(B(t))\\ \Downarrow\\ dX(t) = \frac {d(A(t))}{A(t)} - dln(B(t)) $$

这里注意，\(ln(B(t))\)里面的因子是布朗运动，不是普通的微分，得用伊藤引理来求微分，而且要注意，GBM(链接里面有对应的伊藤公式)是伊藤过程，不是标准的BM，伊藤引理引用的公式是不一样的

下面来求 \(dln(B(t))\)

\begin{equation}\begin{split} dln(B(t))&=f'(B(t))dB(t)+ \frac{1}{2}f''(B(t))B(t)^2{\delta}^2dt\\ &= \frac{1}{B(t)}(\mu B(t)dt+\delta B(t)dZ(t))-\frac{1}{2}{\delta}^2dt\\ &= {\mu}dt+{\delta}dZ(t)-\frac{1}{2}{\delta}^2dt\\ &= ({\mu}-\frac{1}{2}{\delta}^2)dt+{\delta}dZ(t) \end{split}\end{equation}

把\(dln(A(t))\)和\(dX(t)\)代入来求 \(dA(t)\)

$$ k(\theta -X(t))dt+{\eta}dW(t)=\frac {d(A(t))}{A(t)}-({\mu}-\frac{1}{2}{\delta}^2)dt-{\delta}dZ(t)\\ \Downarrow\\ \frac {d(A(t))}{A(t)}=(k(\theta -X(t))+{\mu}-\frac{1}{2}{\delta}^2)dt+{\eta}dW(t)+{\delta}dZ(t)\\ \Downarrow\\ d(A(t))=(k(\theta -X(t))+{\mu}-\frac{1}{2}{\delta}^2)A(t)dt+{\eta}A(t)dW(t)+{\delta}A(t)dZ(t) $$

我就能求到这儿了，和官方的(5)式还是有差别，如果要相等就得有下面这个等式，但是我真不知道怎么求这个等式

$$ {\eta}^2+2{\rho}{\delta}{\eta}+{\delta}^2=0\\ \Downarrow\\ \rho \delta \eta = - \frac { 1 } { 2 } \left( \delta ^ { 2 } + \eta ^ { 2 } \right) $$

其中\({\rho}\)是\(Z(t)\)和\(W(t)\)的相关系数，满足\(dZ(t)dW(t)={\rho}dt\)，然后论文中说\({\rho}{\delta}{\eta}\)来自于\(Z(t)\)和\(W(t)\)的协方差，这个等式成立吗？我是找了各种资料也不知道这个等式是否成立，或者为什么成立。。。。。。

之前的思路是错的，但是我不打算删掉，接下来才是正确的思路，非常感谢知乎大神（消****）的指点

核心思路就是通过B(t)和X(t)来确定A(t)的随机微分方程，因为B和X是已知的。那么会有人讲，A和B都是stock price，不能都定义成GBM吗？如果A也定义成GBM，那么A、B、X间形成不了等式的关系，所以通过B、X来确定A是一个很好的思路。

那么上面的求解思路有什么问题呢？我把A当成普通随机过程了，我怎么知道A里面不含布朗运动呢？只要含布朗运动的微分方程，做微分的链式展开时就和普通的链式展开法则不一样的。所以把A写成B和X的表达式再做Ito展开才是正解。为什么要做Ito展开呢？因为A的表达示里面有B和X，而B和X是已知的Ito过程，所以如果展开必然用Ito展开。

对3式做变换

$$ { A ( t ) = e ^ { x ( t ) } B ( t ) } \qquad (101) \\\\ \Downarrow\\\\ { d A ( t ) = d \left( e ^ { x ( t ) } B ( t ) \right) } \qquad (102) $$

接下来的目标就是从102式推导到5式

$$ d A ( t ) = e ^ { x (t) } d B ( t ) + B ( t ) e ^ { x (t) } d x + e ^ {(x)} d B ( t ) d x ( t ) + \frac { 1 } { 2 } B ( t ) e ^ { x (t) } d x ( t ) d x ( t ) \qquad (103) $$

到103式怎么来的呢？这就是随机分析里面的核心之一：伊藤展开，单元和多元的都很重要，下面列出本文中用到的二元伊藤展开公式，二元就是B和X(金融随机分析 第二卷(中文版) 定理4.6.2)

$$ \begin{aligned} d f ( t , X , Y ) = f _ { t } d t + f _ { x } d X + f _ { y } d Y + \frac { 1 } { 2 } f _ { x x } d X d X + f _ { x y } d X d Y + \frac { 1 } { 2 } f _ { y y } d Y d Y \end{aligned} $$

继续推导

$$ d A ( t ) = e ^ { x (t) }( d B ( t ) + B ( t ) d x + d B ( t ) d x ( t ) + \frac { 1 } { 2 } B ( t ) d x ( t ) d x ( t )) \qquad (104) $$

对104中的部分进行拆解分析，和式中第3部分

$$ \begin{equation} k ( \theta - x ( t ) ) = \alpha\\\\ \begin{split} d B ( t ) d x ( t ) &= \alpha \mu B ( t ) d t d t + \mu \eta B(t) dW(t) dt + \alpha\sigma dZ(t)dt + B(t)\sigma\eta dW(t)dZ(t)\\\\ &= 0+0+0+B(t)\sigma\eta dW(t)dZ(t)\\\\ &= B(t)\rho\sigma\eta dt \end{split} \end{equation} $$

这里用到了随机分析里面很重要的一些等式(金融随机分析 第二卷(中文版) 式4.4.12),其中W(t)泛指布朗运动

$$ d W ( t ) d W ( t ) = d t , \quad d t d W ( t ) = d W ( t ) d t = 0 , \quad d t d t = 0 $$

最后一步用到了\(dW(t)dZ(t)=\rho dt\)，由论文中给出

接下来第4部分

$$ \begin{align} dX(t)dX(t) &= \alpha^{2}dtdt + \eta^{2}dW(t)dW(t) + 2\alpha\eta dW(t)dt\\ &= 0 + \eta^{2}dt + 0\\ &= \eta^{2}dt\\ \end{align}\\ \Downarrow\\ \frac{1}{2}B(t)dX(t)dX(t) = \frac{1}{2}B(t)\eta^{2}dt $$

把上面的结果进行整合，把104式中和式的第1项和第2项展开可得

$$ d A ( t ) = e ^ { x (t) } (\mu B(t)dt+\sigma B(t)dZ(t)+B(t)\alpha dt+\eta B(t)dW(t)+ \rho\sigma\eta B(t)dt+\frac{1}{2}B(t)\eta^{2}dt)\\ \Downarrow\\ dA(t)=e^{x(t)}B(t)(\mu dt+\sigma dZ(t)+\alpha dt+\eta dW(t)+ \rho\sigma\eta dt+\frac{1}{2}\eta^{2}dt)\\ \Downarrow\\ dA(t)=A(t)((\mu +\alpha + \rho\sigma\eta + \frac{1}{2}\eta^{2})dt+\sigma dZ(t)+\eta dW(t))\\ \Downarrow\\ dA(t)=(\mu +k(\theta - X(t)) + \rho\sigma\eta + \frac{1}{2}\eta^{2})A(t)dt+\sigma A(t)dZ(t)+\eta A(t)dW(t) \qquad (5) $$

这样就推到了论文上的5式。

纠正8式，dW(t)前面少了个参数h，推导就是把各式代入进去，太简单了，这里就不写了

$$ d V ( t ) = V ( t ) { [ h ( t ) ( k ( \theta - X ( t ) ) + \frac { 1 } { 2 } \eta ^ { 2 } + \rho \sigma \eta) + r ] d t + \eta d W ( t ) } $$

更正后8式：

$$ d V ( t ) = V ( t ) { [ h ( t ) ( k ( \theta - X ( t ) ) + \frac { 1 } { 2 } \eta ^ { 2 } + \rho \sigma \eta) + r ] d t + h\eta d W ( t ) } $$

所以更正后的 dV(t)为：

$$ dV ( t ) = V ( t ) ( ( h ( t ) ( k ( \theta - X ( t ) ) + \frac { 1 } { 2 } \eta ^ { 2 } + \rho \sigma \eta ) + r ) d t + h\eta d W ( t ) ) $$

三. 建立优化方程(HJB)

先吐个槽，看这篇论文之前完全不懂优化控制这块的东西，就连微积分都不懂，花了老大精力刷了ODE，入门了一下PDE，SDE没有看，然后优化控制，从变分法，Pontryagin极大值原理到HJB动态规划。

结束这一套知识体系的建立后我又拿起这篇论文，发现这里面的HJB是基于SDE二阶的，而我之前看的是基于ODE一阶的，好吧，买了一本随机过程刷了里面的二阶HJB，又拿起论文一看。。。这篇论文里面的控制变量是二维的，我看过的所有的书中都未曾提及。肿么办？

在有点焦急和丧气的时候发现了论文里面某个点对另外一篇论文 《A Stochastic Control Approach to Portfolio Problems With Stochastic Interest Rates》 的引用，看到了里面对二维控制变量HJB的解释，终于找到你了。今天刷完了，也把论文中的HJB推导出来了，那一刻差点感冒。

$$ d Y ( t ) = \Lambda ( t , Y ( t ) , u ( t ) ) d t + \Sigma ( t , Y ( t ) , u ( t ) ) d W ( t ) $$

上面这个议程是状态方程，多维的，我们要按照这个样子把Y(t)=(V(t),X(t))按照这个样子写出来，求出\(\Lambda 和 \Sigma \)的表达式。然后求出HJB方程如下：

$$ A ^ { v } G ( t , y ) : = G _ { t } ( t , y ) + 0,5 \sum _ { i , j = 1 } ^ { n } \Sigma _ { i j } ^ { * } ( t , y , v ) \cdot G _ { y _ { i } y _ { j } } ( t , y ) + \sum _ { i = 1 } ^ { n } \Lambda _ { i } ( t , y , v ) \cdot G _ { y _ { i } } ( t , y ) \\ \sup _ { | v | \leq \delta } A ^ { v } G ( t , x , r ) = 0 \\ G ( T , x , r ) = x ^ { \gamma } $$

推导这个式子应该是在另外一本书中 《Controlled_Markov_Processes_and_Viscosity_Solutions》，好吧，就不深入研究了，能找到这个式子已经很不容易了。

从论文中的V(t)和X(t)可以推出如下等式：

$$ \begin{aligned} Y ( t ) & = ( V ( t ) , X ( t ) ) ^ { T } \\ \Lambda ( t , x , r , h ) & = ( v(h(k(\theta - x) + \frac{1}{2}\eta^{2}+\rho \sigma \eta)+r , k(\theta - x) ) ^ { T } \\ \Sigma ( t , x , r , h ) & = ( hv\eta , \eta ) ^ { T } \\ \Sigma ^ { * } ( t , x , r , h ) & = \left( \begin{array} { c c } { h^{2}v^{2}\eta^{2} } & { hv\eta^{2} } \\ { hv\eta^{2} } & { \eta^{2} } \end{array} \right) \\ A ^ { \pi } G ( t , x , r ) = & G _ { t } + \frac { 1 } { 2 } [ h ^ { 2 } \eta ^ { 2 } v ^ { 2 } G _ { v v } + \eta ^ { 2 } G _ { x x } \\ & + 2 h \eta ^ { 2 } v G _ { v x } ] + [ h k ( \theta - x ) + \frac { 1 } { 2 } h \eta ^ { 2 } \\ & + h \rho \eta \sigma + r ] v G _ { v } - k ( x - \theta ) G _ { x } = 0 \qquad (105) \\ G ( T , v , x ) & = v ^ { \gamma } \qquad (10) \end{aligned} $$

论文中的HJB：

$$ \begin{array} { c } { G _ { t } + \sup\{ \frac { 1 } { 2 } \left[ h ^ { 2 } \eta ^ { 2 } v ^ { 2 } G _ { v v } + \eta ^ { 2 } G _ { x x } \right.} \\ { + 2 h \eta ^ { 2 } v G _ { v x } ] + \left[ h k ( \theta - x ) + \frac { 1 } { 2 } h \eta ^ { 2 } \right.} \\ { + h \rho \eta \sigma + r ] v G _ { v } - k ( x - \theta ) G _ { x } \} = 0 } \end{array} \qquad (9) $$

上面的式子推出来不难，我自己推出来的105和论文中的9有点差别，论文中的sup加在了后面3项，这是为啥？难道后面三项是hamilton函数？还有就是10中的\(v^{\gamma}\)不应该是之前提到过的效用函数\(\frac{1}{\gamma }v^{\gamma}\)?

下面是12式的推导，我也是猜的，就是把hv看做一个变量，9式对hv求导，导数等于0就是12式，但是为什么这么做呢？我也不太清楚

$$ h ^ { * } \eta ^ { 2 } v G _ { v v } + \eta ^ { 2 } G _ { v x } + b G _ { v } = 0 \qquad (12) $$

最终方程

$$ \begin{array} { c } { \eta ^ { 2 } G _ { t } G _ { v v } - \frac { 1 } { 2 } \eta ^ { 4 } G _ { v x } ^ { 2 } - \frac { 1 } { 2 } b ^ { 2 } G _ { v } ^ { 2 } - b \eta ^ { 2 } G _ { v } G _ { v x } } \\ { + \frac { 1 } { 2 } \eta ^ { 4 } G _ { v v } G_ {x x} + r \eta ^ { 2 } v G _ { v } G _ { v v } } \\ { - k ( x - \theta ) \eta ^ { 2 } G _ { x } G _ { v v } = 0 } \end{array} \qquad (14) $$

四. 求解析解

对14式求解，最终是求最优解h

时隔1个多月，发现看之的东西都有点忘了，最近把机器学习全部刷了一篇，花几天时间梳理一下做些输出，顺便把之前的这篇Q入门神作写完。

按论文[5]中的方法把value function G写成如下形式，具体原因暂时不深究了

$$ G(t, v, x)=f(t, x) v^{\gamma} \qquad (15) $$

这样就有终点条件：

$$ f(T, x)=1 \quad \forall x \qquad (16) $$

为什么呢？因为之前10式告诉我们终点条件为：\(v^{\gamma}\)

这里重点介绍一下17式，这里主要的数学点就是偏微分，偏微分主要考虑的是参数中含有的变量，看15式，G的参数含有t,v,x，f的参数含有t,x，参数含有的变量才能做微分，不然微分的值就是0

那么14式如何到17式呢？先把G对t,v,vv,xx,x,vx的偏微分求出来，其中vv,xx,vx是二阶偏微分

$$ G_t = v^{\gamma} f_t \qquad G_v=\gamma \nu^{\gamma -1} f $$ $$ G_{vv} = \gamma (\gamma -1)v^{\gamma -2}f \qquad G_xx=\nu^{\gamma } f_{xx} $$ $$ G_{vx} = \gamma v^{\gamma -1}f_x \qquad G_x = v^{\gamma}f_x $$

然后带入14可以求出17式，这个我手算过，确实可以。

$$ \begin{array}{l}{(\gamma-1) \eta^{2} f f_{t}-\frac{1}{2} \gamma \eta^{4} f_{x}^{2}-\frac{1}{2} \gamma b^{2} f^{2}-\frac{1}{2} \gamma \eta^{4} f f_{x}} \\ {\quad-\gamma \rho \sigma \eta^{3} f f_{x}+\frac{1}{2}(\gamma-1) \eta^{4} f f_{x x}} \\ {\quad+\gamma(\gamma-1) r \eta^{2} f^{2}+k(x-\theta) \eta^{2} f f_{x}=0}\end{array} \qquad (17) $$

后面的我就不敢算了，计算量太大了。。。后面想学一下matlab计算一下的，被一朋友劝放弃了，哈哈。

然后我们就直接到解 h

$$ \begin{array}{l}{\alpha(t)=\frac{k(1-\sqrt{1-\gamma})}{2 \eta^{2}}.} \\ {\left\{1+\frac{2 \sqrt{1-\gamma}}{1-\sqrt{1-\gamma}-(1+\sqrt{1-\gamma}) \exp \left(\frac{2 k(T-t)}{\sqrt{1-\gamma}}\right)}\right\}}\end{array} \qquad (24) $$ $$ \begin{array}{c}{\beta(t)=\frac{1}{2 \eta^{2}\left[(1-\sqrt{1-\gamma})-(1+\sqrt{1-\gamma}) \exp \left(\frac{2 k(T-t)}{\sqrt{1-\gamma}}\right)\right]}.} \\ {\left\{\gamma \sqrt{1-\gamma}\left(\eta^{2}+2 \rho \sigma \eta\right)\left[1-\exp \left(\frac{2 k(T-t)}{\sqrt{1-\gamma}}\right)\right]^{2}\right.} \\ {-\gamma\left(\eta^{2}+2 \rho \sigma \eta+2 k \theta\right)\left[1-\exp \left(\frac{2 k(T-t)}{\sqrt{1-\gamma}}\right)\right]} \end{array} \qquad (25) $$ $$ h^{*}(t, x)=\frac{1}{1-\gamma}\left[\beta(t)+2 x \alpha(t)-\frac{k(x-\theta)}{\eta^{2}}+\frac{\rho \sigma}{\eta}+\frac{1}{2}\right] \qquad (28) $$

上面这3个式子非常重要，程序复现时需要

五. 复现

其实我看到这里的时候我差点崩溃了，几个月的时间啊，竟然用造出来的假数据来做复现，开玩笑的吧。。。。。。

当然该做的还是得做，我先告诉大家结果，哈哈

模拟数据：

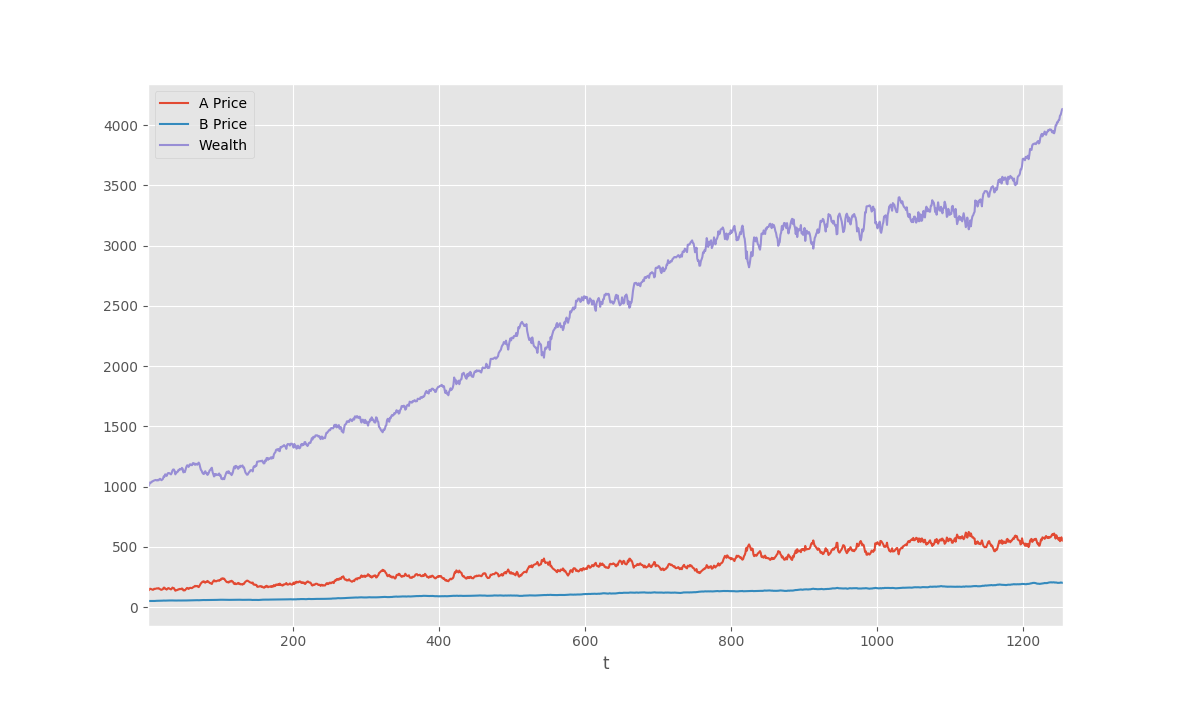
实际期货数据：

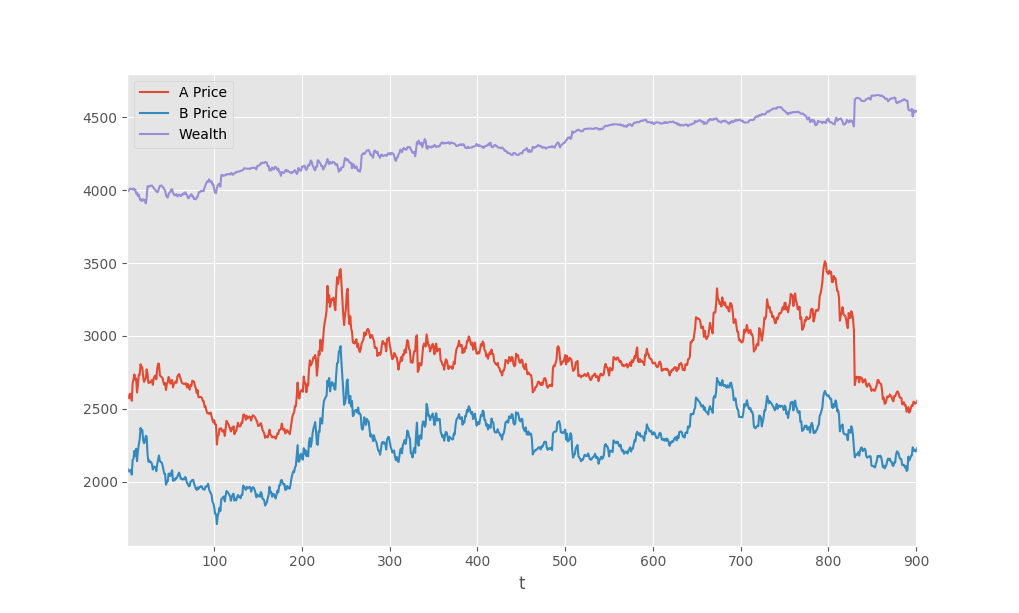
虽然实际数据的收益率非常低，但是波动并不高，我试过一些数据，波动都不高。

其实实际数据的核心在于B资产的价格越符合GBM越好，A和B资产的价差越符合正态分布越好，这个资产选择嘛就要靠自己发掘了。

选择好资产后就要用Appendix里面的最大似然估计了，把参数估计出来代进公式计算。

能把这篇论文分析出来，而且用代码复现出来，效果也没有很糟，我已经很感动了，几个月的烧脑没有白费。而且这个算法到代码中间是需要做一些调整的，我把脑袋都想破了不断反复的测试那几个公式才分析出来调整点在哪儿，刚把东西调出来时我都差点儿哭了。

之前刷强化学习的时候看到有model based的强化学习，我想到时能不能把这些东西和rl结合起来，不过只是个想法，估计实施起来有点困难。

2019.3.28 纪念量化之路两年还未放弃