学习时间序列分析的前置基础知识

不管是高频数据还是中低频数据都是标准的时间序列数据，而且看知乎上确实有一些机构用时间序列的回归方法做到了盈利，所以为了进一步发展决定还是学习一下，其实书早就已经买了，但是之前翻了两页，公式啥的太多了一看就头晕，这两天决定突破一下，你知道这种专业的书籍不是看书就行的，最好是有懂行的人帮你讲，可是术业有专攻，很多我认识的朋友不是搞这个领域的，木有办法，现在还是靠度娘吧。

现在把我这两天学习到的成果以最简单的方式程现出来，有些我就直接贴链接了

方差，标准差(STDEV)

标准差 = 方差 的开方

了解这个概念主要是相对于MA来讲的（算术移动平均线），现在有些策略属于突破策略，普罗大众都用短期均线突破长期均线来判断买卖点，但是有一个东西叫标准差，我之前不太了解细节时觉得没啥用，而且当时在Trading System and Methods这本书第一章的基本概念里面就看到过，没太引起重视，主要是没有实际操盘经验，这次引起重视是在知乎上看到了一位大神的文章里面说他的策略用到了标准差，BOLL通道也用的标准差进行的计算，这里我才回想起知乎上一个cta大神以前说过，最基础的先把这些基础指标过一下，是啊，我算是偷懒了。

标准差是方差的开根号，为什么要用标准差而不是直接方差，因为方差是把当前的离散程度做了一个平方的，这样会导致离散程度的偏差过大。标准差，MA等等都是表示数据的离散程度的，做离散程序分析是需要关注这些概念的。

协方差(Covariance)，相关系数

不讲数据含义了，对现在的我来讲意义不大，主要是描述两组变量变化的方向是否一致，一致就是正数，不相关（一个往北，一个往东或者是西）就是0,负相关（一个往东一个往西）就是负数，但是纯的协方差计算出来的值意义不是特别大，因为很可能两组变量变化的方向一致，但是量不一样，这样会导致数值计算出来特别大，这样就引申出来了相关系数的概念，协方差/标准差的积，这样算出来是在-1~1之间，可以很好的量化出两组数据的相关性。

我这么一两句讲的不是很透彻，来看看大神的讲解：

非常形象的讲解

相关系数分两种：Pearson（皮尔逊）和 Spearman Rank（斯皮尔曼等级）相关系数

斯皮尔曼相关系数对于数据错误和极端值的反应不敏感，在金融中可能 Spearman 更实用

import pandas as pd
import scipy.stats as stats

# Pearson

pd.corr()

# Spearman 将数据先做rank，也就是分等级( [1.2, 3.4, 1.3] -> [1,3,2] )再做 Pearson
r_s = stats.spearmanr(Y, X)
print 'Spearman Rank Coefficient: ', r_s[0]
print 'p-value: ', r_s[1]
# p-value 常规用法 小于 0.05 说明存在相关性， 反之说明没相关性

矩

不是矩阵哦，符号是E(x)，期望值(Expectation)，基础概念，很多地方要用到，标准差是二阶中心矩，一阶就是均值(期望值)

我不罗嗦了，来大神：

非常形象的讲解

log return

经常在知乎上看到这个词，感觉很高大上。和log return对标的是simple return（简单收益率），就是 尾-头/头 的计算收益率的方法，这个概念也是基础，后面经常用到，对统计和分析有着不错的影响。

好处： 1. 可以简单的做加减操作，做统计很方便 2. 当数值很小时非常接近简单收益率

基础公式可以

e = 2.71828 (自然常数)
Ln(x) 以e为底求对数
exp(x) e的x次方

来大神链接：

实例讲解，可以同时看看上面其他的回答

概念性的，看第一个回答

用积分的概念讲解，我也不是特别理解

平稳序列

简单来讲就是一条放平了的直线，但允许有波动，均值和标准差一直不变。做后面所有的分析都要基于平稳序列，如果股票价格是平稳序列，世界将会怎样？均值不变，那么肯定做回归策略，必定赚钱。

检测方法 Dickey-Fuller test

from statsmodels.tsa.stattools import adfuller

# Compute the p-value of the Dickey-Fuller statistic to test the null hypothesis that yw has a unit root
print adfuller(yw)[1]

# 小于0.05则是平稳序列

协整

利用协整套利

股票价格为非平稳序列，y为某支股票，x为某支股票，但是

yt-rxt 为平稳序列 r为协整系数

这种关系称为协整(cointegration)，现主要用于套利。

import statsmodels.api as sm

result = sm.tsa.stattools.coint(stock1, stock2)
pvalue=result[1]
#如果pvalue<0.05则说明高相关性

再用线性回归算出r

x = stock_df1
y = stock_df2
X = sm.add_constant(x) 
result = (sm.OLS(y,X)).fit()
print(result.summary())

找到股票名对应的coef则为系数，const为常量，这里不用管

正态分布

正统的概念我就不写了，这里主要讲3方面

Skewness（偏度）

import scipy.stats as stats

# symmetric distribution has skew 0
skewness = stats.skew(returns)

主要是讲那个尖是在正常的左边，还是右边

左边是负偏(Negatively) mean < median < mode，但是skew值是大于0的

右边是正偏(Positively skewed) mean > median > mode，skew值是小于0

Kurtosis（峰度）

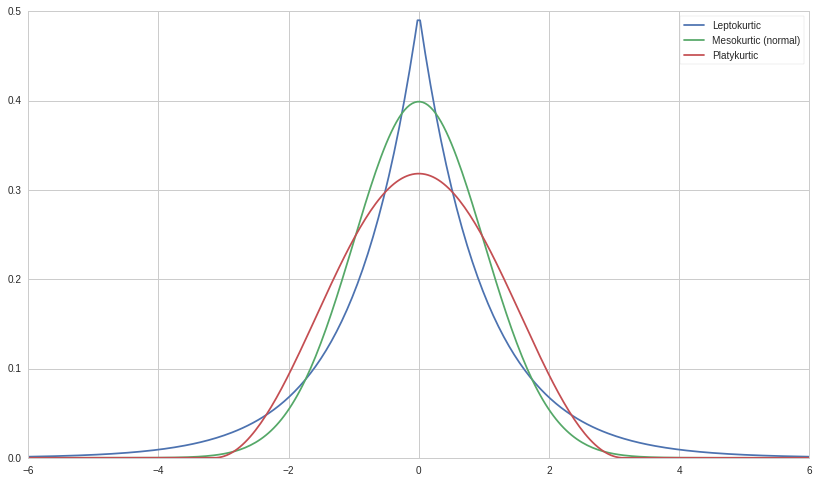
峰度 kurtosis 大于0说明是有尖峰和肥尾的

尖峰一定有肥尾？如果两个分布的mean和方差一样，那么相对来讲是有肥尾的

import scipy.stats as stats

# kurtosis 0 is normal
kurtosis = stats.kurtosis(returns)

kurtosis > 0 leptokurtic
kurtosis < 0 platykurtic

检测是否符合正态分布

from statsmodels.stats.stattools import jarque_bera

# 这里的kurtosis值，标准是3
_, pvalue, skewness, kurtosis = jarque_bera(returns)


if pvalue > 0.05:
    print 'The returns are likely normal.'
else:
    print 'The returns are likely not normal.'

检测异方差(残差没有固定的方差，不服从正态分布)

# Artificially create dataset with changing variance around a line
y2 = xs*(1 + .5*np.random.randn(100))

# Perform linear regression
slr2 = regression.linear_model.OLS(y2, sm.add_constant(xs)).fit()
fit2 = slr2.params[0] + slr2.params[1]*xs

...

residuals1 = y1-fit1
residuals2 = y2-fit2

xs_with_constant = sm.add_constant(xs)

_, pvalue1, _, _ = stats.diagnostic.het_breushpagan(residuals1, xs_with_constant)
_, pvalue2, _, _ = stats.diagnostic.het_breushpagan(residuals2, xs_with_constant)
# pvalue1 normal  pvalue2 unnormal
print "p-value for residuals1 being heteroskedastic", pvalue1
print "p-value for residuals2 being heteroskedastic", pvalue2
# 大于0.05就是服从正态分布,残差不是异方差
p-value for residuals1 being heteroskedastic 0.740534744151
p-value for residuals2 being heteroskedastic 3.85868174966e-06

# 异方差越明显说明可能不是性关系，如果没有异方差可能就是线性关系

# 异方差调整
slr2.get_robustcov_results().summary()

model = sm.OLS(Y_heteroscedastic, sm.add_constant(X)).fit()
breusch_pagan_p = smd.het_breushpagan(model.resid, model.model.exog)[1]

检测残差的自相关性

# Load pricing data for an asset
start = '2014-01-01'
end = '2015-01-01'
y = get_pricing('DAL', fields='price', start_date=start, end_date=end)
x = np.arange(len(y))

# Regress pricing data against time
model = regression.linear_model.OLS(y, sm.add_constant(x)).fit()

model.summary()

在summary中有一项是 Durbin-Watson

DW是0<D<4,统计学意义如下：

当残差与自变量互为独立时，D=2 或 DW 越接近2，判断无自相关性把握越大。
当相邻两点的残差为正相关时，D<2，DW 越接近于0，正自相关性越强。
当相邻两点的残差为负相关时，D>2，DW 越接近于4，负自相关性越强。

某序列的自相关性

# 参考 https://blog.csdn.net/u010414589/article/details/49622625

acf, acf_confs, prices_qstats, prices_qstat_pvalues = statsmodels.tsa.stattools.acf(y, qstat=True, nlags=10)

# (p)acf 就是每个nlag的相关系数， (p)acf_confs 是置信区间

# 部分自相关
pacf, pacf_confs = statsmodels.tsa.stattools.pacf(y, nlags=10)

# prices_qstat_pvalues 里面有每一lag的pvalues，小于0.05则就是自相关，否则不是自相关
# 因为在某个序列里面也可能出现某一段自相关性强，某一段不强，所以是一个序列的pvalue，而不是一个

import statsmodels.stats.diagnostic as smd

model = sm.OLS(Y_autocorrelated, sm.add_constant(X)).fit()
B0, B1 = model.params
residuals = model.resid

ljung_box = smd.acorr_ljungbox(residuals, lags = 10)
print "Lagrange Multiplier Statistics:", ljung_box[0]
print "\nP-values:", ljung_box[1], "\n"

if any(ljung_box[1] < 0.05):
    print "The residuals are autocorrelated."
else:
    print "The residuals are not autocorrelated."

失效模式的标准误(std err)调整

存在异方差，且异方差形式未知时，而且残差或者自变量还有可能自相关，这时候可以用newey-west对结果进行调整，因为本来有异方差时模式是要失效的，调整后还是可以取其中的值进行参考的，让它更具有统计意义

# Regress pricing data against time
model = regression.linear_model.OLS(y, sm.add_constant(x)).fit()
...

from math import sqrt

# Find the covariance matrix of the coefficients
cov_mat = stats.sandwich_covariance.cov_hac(model)

# Print the standard errors of each coefficient from the original model and from the adjustment
print 'Old standard errors:', model.bse[0], model.bse[1]
print 'Adjusted standard errors:', sqrt(cov_mat[0,0]), sqrt(cov_mat[1,1])

多重共线性(自变量相关)

基本检测：如果R平方值很高(模型好)但是t-statistics小(参数不准确)，说明，模型可信度高，但是参数的预测不准确，这样有可能就是多重共线性。

进一步检测：去掉某自变量，看会不会在不影响R平方值的情况下而提高t-statistics

其实把自变量做一个相关性检测也是一项基本检测。

判断某一时间序列的回归特性

方法：Hurst exponent ，用法见代码里面的注释

这个指标与分形有关，可能不是这么用的，具体看带你正确理解 Hurst 指数和分数布朗运动

"""
    Hurst exponent helps test whether the time series is:
    (1) A Random Walk (H ~ 0.5)
    (2) Trending (H > 0.5)
    (3) Mean reverting (H < 0.5)
"""
def hurst(context, data, sid):
    # Gathers all the prices that you need
    gather_prices(context, data, sid, 40)
    # Checks whether data exists
    data_gathered = gather_data(data)
    if data_gathered is None:
        return    

    tau, lagvec = [], []
    # Step through the different lags
    for lag in range(2,20):  
        # Produce price different with lag
        pp = numpy.subtract(context.past_prices[lag:],context.past_prices[:-lag])
        # Write the different lags into a vector
        lagvec.append(lag)
        # Calculate the variance of the difference
        tau.append(numpy.sqrt(numpy.std(pp)))
    # Linear fit to a double-log graph to get power
    m = numpy.polyfit(numpy.log10(lagvec),numpy.log10(tau),1)
    # Calculate hurst
    hurst = m[0]*2

    return hurst

置信区间

置信区间的产生要是数据符合正态分布，或者t分布才有意义

heights = np.random.normal(POPULATION_MU, POPULATION_SIGMA, s)
SE = np.std(heights) / np.sqrt(s)
print stats.norm.interval(0.95, loc=mean_height, scale=SE)

ARIMA

做时序预测，要为平稳序列，下面为使用方法，理论请看书。

X = series.values
size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)]
history = [x for x in train]
predictions = list()
for t in range(len(test)):
    model = ARIMA(history, order=(5, 1, 0))
    model_fit = model.fit(disp=0)
    output = model_fit.forecast()
    yhat = output[0][0]
    predictions.append(yhat)
    obs = test[t]
    history.append(obs)