Population Stability Index (PSI) 稳定度指标
$$P S I = \sum \left( f _ { \text { development } } ^ { i } - f _ { \text {validation} } ^ { i } \right) * \ln \left( f _ { \text {development} } ^ { i } / f _ { \text {validation} } ^ { i } \right)$$
概念简单,表明某时刻某群体真实值和预测模型间的偏离度。
study: Bank case PSI, PSI
实际策略:PSI5 mean reversion
这个策略没有源码和思路,只是说是用的统计学教科书中关于股价的公式来做的,而且是用的PSI回归模型,我猜是用的PSI计算的一个指标,偏离多少必回归,然后开仓。
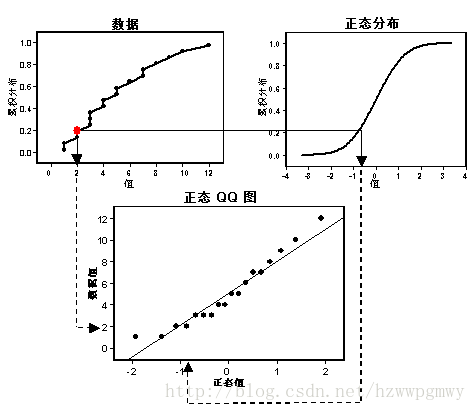
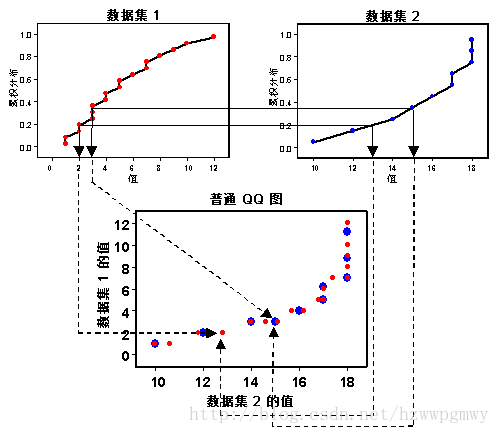
QQ 图
判定是否为正态分布 (scipy.stats.probplot)
期望值的近似
在强化学习中需要知道某个action后导致的tao,这个tao就是后面一系列的动作(episode),需要知道出现某个action后产生tao的概率。然后把每种tao产生的reward乘以tao出现的概率,求期望值,其实就是加权平均嘛
这个很难计算的,这样就可以用如下方法来近似,直接用这个action玩N次游戏,把所有的reward加起来,除以N,即可近似出这个期望值
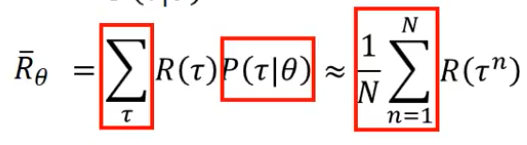
正态分布 -> 均匀分布
一个正态分布的向量 通过对应正态分布的CDF进行转换就可以得到均匀分布 概率积分变换
library(MASS)
set.seed(100)
m <- 3
n <- 2000
# 产生mu=0 std=1的互有相关性的正态分布的3维向量
sigma <- matrix(c(1, 0.4, 0.2,
0.4, 1, -0.8,
0.2, -0.8, 1),
nrow=3)
z <- mvrnorm(n,mu=rep(0, m),Sigma=sigma,empirical=T)
library(psych)
cor(z,method='spearman')
pairs.panels(z)
# 上面显示的是正态分布
# pnorm 就是通过mean=0 std=1的正态分布的cdf来求z中每个变量的概率
u <- pnorm(z)
pairs.panels(u)
# 这里显示的就是均匀分布
价格变化分布
(取自于Advanced ML in Finance page 27)
固定时间内的价格变化
这个一直是高斯分布,其实最贴切的应该是 Generalized Pareto Distribution,最能匹配尖峰肥尾。
GPD对应的R包SpatialExtremes下载(如果2.0-7.1编译出错,安装7.0版本)
这里有一篇用R分析收益率的文章Exploring Heavy Tails Pareto and Generalized Pareto Distributions
packageurl <- "https://cloud.r-project.org/src/contrib/SpatialExtremes_2.0-7.tar.gz"
install.packages(packageurl, repos=NULL, type="source")
# 安装 Rsafd 包
install.packages("Rsafd", repos="http://R-Forge.R-project.org")
'''
通过这种方式安装的 Rsafd 是1.2版和 随书的1.0版不一样
1.0 的 fit.gpd 等于 1.2的gpd.tail
1.0 的 pgpd 等等 1.2的gpd.1p
'''
但是这个分布貌似只有一边,非对称,难道要把正收益和abs(负收益)分开匹配?
这个GPD只能分析尾巴,中间部分如果符合正态是不需要分析的。而且是只能分析右尾,分析左尾得把数据做abs
固定成交量(额)内的价格变化
高斯分布
copula
必须要细致的看一下 wikipedia
概念不必再描述,注意点:
- 前提是时间序列要是平稳且连续的,如果有自相关,可能计算出来的copula是错误的
- 分类: gaussian, archimedean(阿基米德), student-t 。 其中 archimedean 含 有很多子类(Clayton, Gumbel, Grank)
Comments
comments powered by Disqus